面向对象设计与构造OO：Unit1-表达式展开

0 前言

第一单元的内容聚焦在对数学意义上的表达式结构进行建模，完成多项式的括号展开与函数调用、化简，体会层次化设计的思想的应用和工程实现。本单元最难理解的部分，我认为是递归下降算法；最难操作的部分，是多项式的化简以及不断增加的迭代需求。

本文将分别介绍分析三次迭代作业，每部分包括需求说明、项目结构、架构设计、性能度量、bug 分析等。最后总结心得体会。

1 第一次作业

1.1 需求说明

第一次作业需要读入一个包含加、减、乘、乘方以及括号（不支持嵌套括号） 的单变量表达式，输出展开括号后的表达式。

在数学层面，课程组已经对表达式的解析层级进行了建模，给出了对应的 BNF 形式化表述，在这里笔者简单声明一下基本概念：

因子 Factor：分为变量因子、常数因子、表达式因子，可以认为是表达式的最基本组分。其中变量因子只有幂函数一种形式（x^3），常数因子是带符号的整数（+233）、表达式因子是带括号的指数式（(x+1)^2）。
项 Term：几个因子相乘，如 -x*3。
表达式 Expression：几个项相加减，如 -1+x^233-2*x。

1.2 项目结构

1.2.1 文件树

src
│  Computer.java
│  Lexer.java
│  MainClass.java
│  Optimizer.java
│  Parser.java
│
├─expr
│      Expr.java
│      Factor.java
│      Number.java
│      Power.java
│      Term.java
│      Variate.java
│
└─poly
        Monomial.java
        Polynomial.java

1.2.2 UML 类图

为方便呈现，仅展示必要的属性和方法。

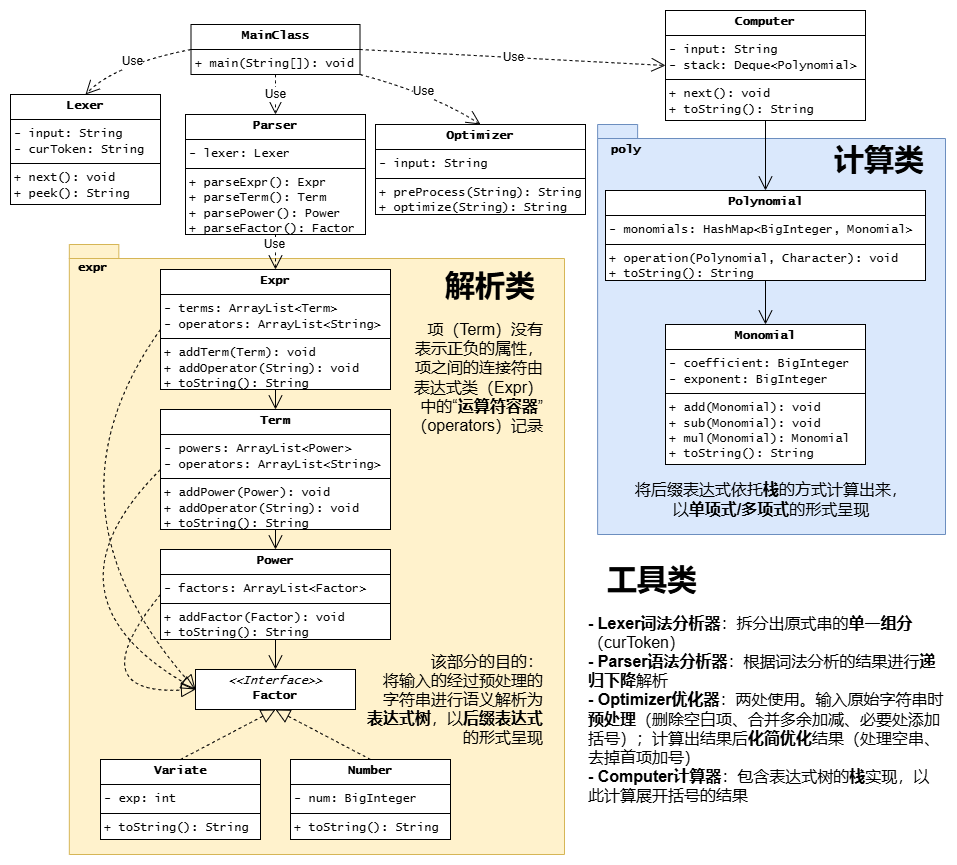
1.3 架构设计

使用了常规的递归下降算法架构，由训练栏目的 advance 代码改编而来（原代码是读入包含加法、乘法和括号的算式，输出后缀表达式）。宏观上讲，流程为：预处理、得到后缀表达式、计算、化简。

1.3.1 预处理

因为输入的原始字符串含有许多空白项（<space> 和 \t） ，且有许多加减号重复的情况，在这里笔者对其进行了预处理，结果是得到不含空白、不含多余加减、不含前导零的原始表达式。这些部分在 Optimizer.preProcess() 中实现。

实际上这里无需处理前导零，因为读入 BigInteger 的时候就被处理了。

其中借助了正则表达式，具体代码：

// delete space and tab  
String delSpaceTab = input.replaceAll("[ \t]", "");  
// merge repeated add and sub  
Matcher matcher = Pattern.compile("[\\+|-]{2,}").matcher(delSpaceTab);
while (matcher.find()) {  
    String repeatAddSub = matcher.group(0);
    // ...
}

1.3.2 得到后缀表达式

接下来经过 Lexer 和 Parser 的递归下降解析便可以得到表达式树。因为笔者当时对于递归下降并没有很深的理解，只能勉强明确是建树的过程，所以在这里多开了一部“输出后缀表达式”。在往届博客中也有部分学长学姐借助了后缀表达式，我认为这是便于新手理解的一种思路。

在这个部分笔者加了一个 Power 部分，目的是与乘法的优先级区分开。可以这么理解：parseExpr 是按 +、- 拆，parseTerm 是按 * 拆，parsePower 是按 ^ 拆，parseFactor 便是读取最底层的因子了。

对于加减法的区分，笔者在 Expr 类中加了 operations 容器，存储项与项之间的连接符是加或减。

// Parser 类
public Expr parseExpr() {  
    Expr expr = new Expr();  
    expr.addTerm(parseTerm());  
  
    while (lexer.peek().equals("+") || lexer.peek().equals("-")) {  
        expr.addOperator(lexer.peek());  
        lexer.next();  
        expr.addTerm(parseTerm());  
    }  
    return expr;  
}  
  
public Term parseTerm() {  
    Term term = new Term();  
    term.addPower(parsePower());  
  
    while (lexer.peek().equals("*")) {  
        // ...
    }  
    return term;  
}  
  
public Power parsePower() {  
    Power power = new Power();  
    power.addFactor(parseFactor());  
  
    while (lexer.peek().equals("^")) {  
        // ...
    }  
    return power;  
}  
  
public Factor parseFactor() {  
    if (lexer.peek().equals("(")) {  
        // ...
        return expr;  
    } else if (lexer.peek().charAt(0) == 'x') {  
        // ...
        return new Variate(exp);  
    } else {  
        // ...
        return new Number(num);  
    }  
}

1.3.3 计算

为了便于复杂组分之间的四则运算，引入了单项式 Monomial 的概念：

这个模型可以表示所有展开化简后的项。

对应的，还有多项式 Polynomial 的概念：

加减号的信息已经在单项式的系数中被记录，多项式无需关心。为了方便索引元素，笔者使用了 <exponent, monomial> 的键值对存储所有单项式。

上一步得到了后缀表达式字符串（用括号分割不同组分），便可直接用栈来计算结果了。这一步依托 Computer 实现，首先读取后缀表达式一个元素，如果不是操作符，将其转换为多项式 Polynomial 并入栈；如果是操作符，取出栈内两个多项式并计算后入栈，直到栈内只剩一个元素，此元素就是最终的多项式结果。

// Computer 类
public void next() {  
    if (pos == input.length()) {  
        return;  
    }  
  
    char c = input.charAt(pos);  
    if (Character.isDigit(c)) {  
        // ...
        this.stack.push(ansPoly);  
    } else if (c == 'x') {  
        // ...
        this.stack.push(ansPoly);  
    } else if (c == '+') {  
        // ...
    } // else if ...
 
    pos++;  
    this.next();  
}

1.3.4 化简

如果表达式第一个字符是 + ，删除之；
如果表达式第一个字符是 - ，且表达式内存在 + ，将这一项移到最前；
如果出现 ^1 ，删除之；
如果出现 1* ，删除之；
此外还有和 0 相关的各种化简。

总的来说，第一次作业是有明确的最短长度的，按照基本规则化简即可。

1.3.5 架构的优缺点

存在的问题：

预处理部分过于臃肿。实际上，对于前导零和多重加减的处理是没必要的。倘若严格按照形式化表述的结构进行解析，这些东西都是没必要的，甚至于空白项的处理。但是考虑到空白项去除很方便，replaceAll 即可，因此在预处理阶段去除空白项是明智的；但去除多重加减就有些不够优雅了（在第三次作业中尝试了 replace 两两成对的，效果还可以）；此外该架构中还进行了去除前导零、给指数前加括号等等操作，有点像面向过程编程了（在第二次作业中大大优化）。
后缀表达式的可迭代性不高。后缀表达式适用于只有加减乘和乘方的式子，但对于后续作业出现的三角函数等有些难以处理。
没有严格按照形式化表述解析。因为笔者是从训练代码改过来的，有许多不适应形式化表述的情况，导致出现一些意想不到的 bug。

优点：可以处理嵌套括号，便于后续迭代。

1.4 性能度量

代码规模：

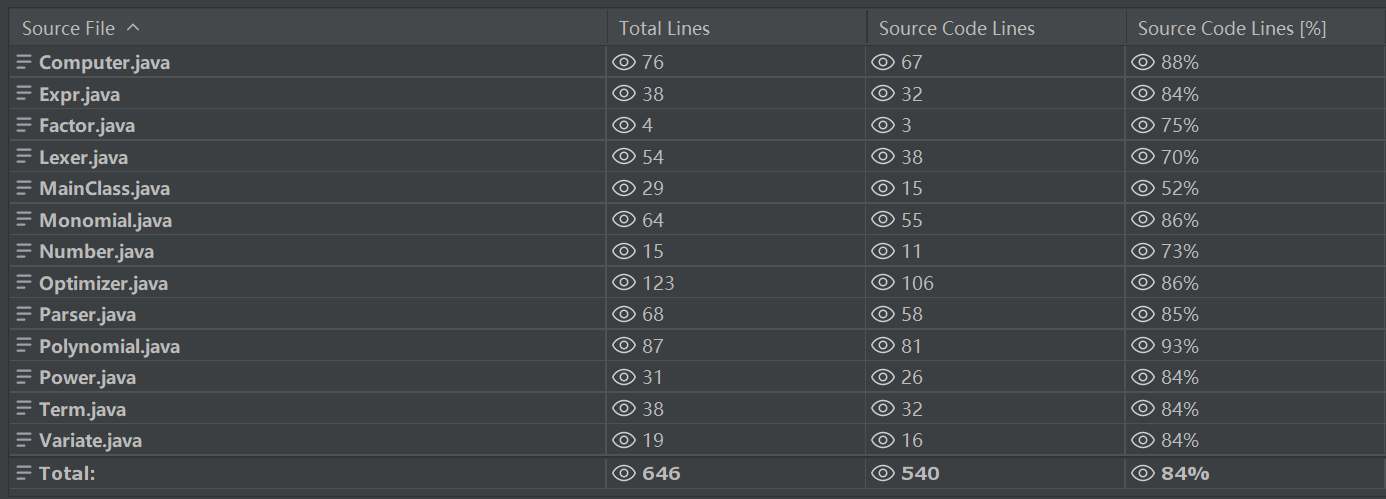
内聚度：笔者使用 DesigniteJava 插件进行代码质量分析，指标含义如下：

LCOM(Lack of Cohesion in Methods)：方法的内聚缺乏度。值越大，说明内聚度越小
FANIN(Fan-in)：类的扇入。值越大，说明模块的复用性越好
FANOUT(Fan-out)：类的扇出。值越大，说明模块复杂度越高

设计要求高内聚低耦合，即 LCOM 值要小，FANIN 值要大，FANOUT 值要合理。

Type Name	LCOM	FANIN	FANOUT
Computer	0	1	2
Lexer	0	2	0
MainClass	-1	0	4
Optimizer	0	1	0
Parser	0	1	5
Expr	0	1	1
Factor	-1	2	0
Number	0	0	0
Power	0	2	1
Term	0	2	1
Variate	0	0	0
Monomial	0	3	1
Polynomial	0	2	2

对于“高内聚低耦合”的理念实现的较好，体现在预处理、建树、计算、化简四部分各司其职；但存在某些方法内部过于臃肿的情况。

1.5 bug 分析

对于 x*+2 这种格式的处理出现 bug。原因：解析表达式的结构没有严格遵循形式化表述，而是“哪错了补哪”的策略。

hack 别人代码的过程中，发现了对于计算出“0”的表达式处理不当的情况，例如：1-1。这一部分笔者处理方式为特判空串并输出。

2 第二次作业

2.1 需求说明

在之前的基础上，读入自定义递推函数的定义以及一个包含幂函数、三角函数、自定义递推函数调用的表达式，输出展开括号（支持嵌套括号）后的结果。

形式化表述新增：

三角函数：属于变量因子。三角函数括号内是因子，类型由 sin ，cos，包含指数。例如 sin((2*x))^2
自定义递推函数：属于变量因子。首先读入递推定义，例如

1
2
3

f{0}(x, y) = x - y
f{n}(x, y) = 0*f{n-1}(x, y) + 35*f{n-2}(x, y^2)
f{1}(x, y) = x^3 + y

在表达式中以 f{5}(-1, sin(x^2) 的形式调用。

2.2 项目结构

2.2.1 文件树

src
│  MainClass.java
│
├─expr
│  │  Const.java
│  │  Expr.java
│  │  Factor.java
│  │  RecurDefine.java
│  │  SubExpr.java
│  │  Term.java
│  │
│  └─vari
│          Power.java
│          Recur.java
│          Trigo.java
│          Vari.java
│
├─parser
│      Definer.java
│      Lexer.java
│      Parser.java
│
└─poly
        Mono.java
        Poly.java

2.2.2 UML 类图

为方便呈现，仅展示必要的属性和方法。

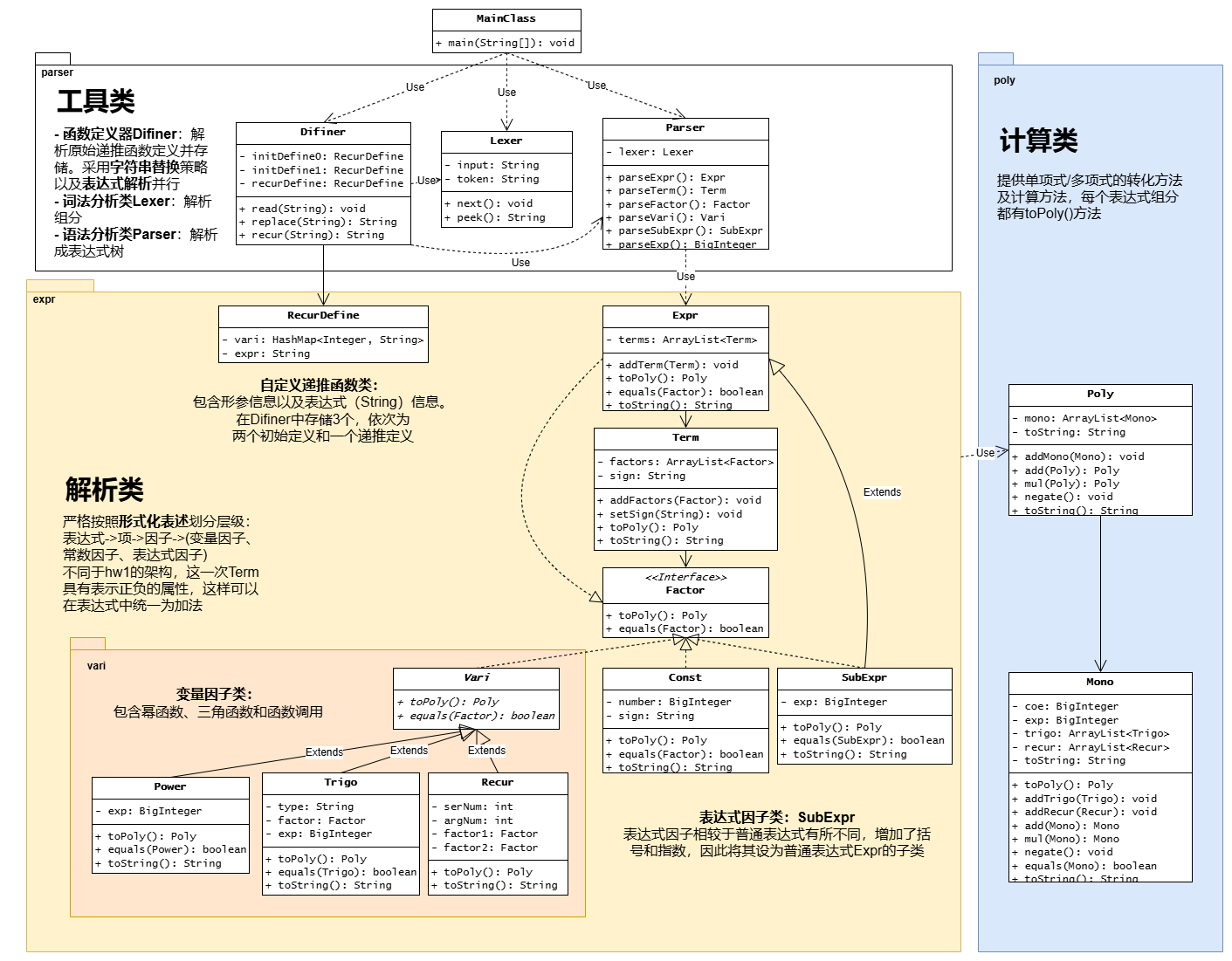
2.3 架构设计

第一次作业中的架构可扩展性实在不高，因此笔者进行了重构，严格遵照形式化表述进行层级解析。

针对新增的递推函数，使用了字符串替换的方式；而对于新增的三角函数，对单项式的定义进行了扩充。

2.3.1 读取递推函数定义

递推函数定义有三行，其中两个初始定义，一个递推定义。在 Definer 类中，定义了 initDefine0 、initDefine1、recurDefine 三个属性，分别表示 f{0} 、f{1} 和 f{n} 。

这三个属性的类型都是 RecurDefine 。这是一个表示单个递推函数定义的类，一个 vari 容器进行“0、1”与“x，y”的键值对匹配，一个字符串 expr 存储相应的表达式。

为了优化性能加快运行速度，笔者对符合“单变量”的递推定义的表达式进行了一次表达式解析，最终的字符串结果进行存储。这么做的好处是，倘若原始定义很复杂，但进行展开化简后很简单，那么接下来进行字符串替换的时候结果也会对应简单。因为 Lexer 和 Parser 已经写的很成熟了，直接调用即可。同时，为了能够处理包含 f{n-1} 和 f{n-2} 的表达式，需要新增相应的处理逻辑。倘若加入 y 的变量解析方式，更是能处理双变量的表达式，但是笔者时间有限并没有对这个进行处理。

public void read(String input) {  
    int equal = input.indexOf('=');  
    String vari = input.substring(5, equal - 1);  
    String expr = input.substring(equal + 1);  
    if (Character.isDigit(input.charAt(2))) {  
        // ...
    } // else ...
}

2.3.2 替换递推函数调用

接下来读取原始字符串，检测其中的递推函数调用组分，并进行替换，直到字符串中不包含 f 。

2.3.3 解析表达式

本次作业架构严格按照形式化表述进行层级划分。体现在因子 Factor 可以分为变量因子 Vari、常数因子 Const、表达式因子 SubExpr；而变量因子又可以进一步分为幂函数 Power、三角函数 Trigo、递推函数 Recur。

在面向对象的设计中，笔者将 Factor 设为接口，Vari 类、Expr 类、Const 类以及 SubExpr 类实现这个接口；而 Vari 类又作为父类，派生出 Power、Trigo、Recur 三个子类。因为表达式因子相当于表达式，仅仅增加了括号和指数，所以 SubExpr 被设计成 Expr 的子类。

2.3.4 计算多项式并输出

本次作业对单项式的定义进行了补充修正：

其中
$或者$

同时，对于单项式和多项式的加减乘运算，在上一次作业中采用在原对象上修改属性的方式，在这一次作业中采用了返回一个新的对象的方式。这么做或许避免了深浅克隆带来的隐患，且更符合“属性对外不可见”的思想。

2.3.5 架构的优缺点

优点：可扩展性高。因为是严格按照形式化表述进行解析的，即便之后加入新的组分也能很快完成代码修改。
架构存在的问题：

对于递推函数的处理有些囫囵吞枣。暴力的字符串替换而非按照形式化表述进行解析，会出现奇怪的不兼容问题，且替换过程并不优雅。
化简逻辑过于简单，不便于应对复杂的三角函数需求。其中单项式的三角函数容器使用 ArrayList 进行存储，增加了运行速度，如果能换成 HashMap 可能会优化性能。

但还是建议以准确性第一，性能永远是第二位的。特别是本次作业中对于性能的追求性价比远远小于保证准确性。

2.4 性能度量

代码规模：

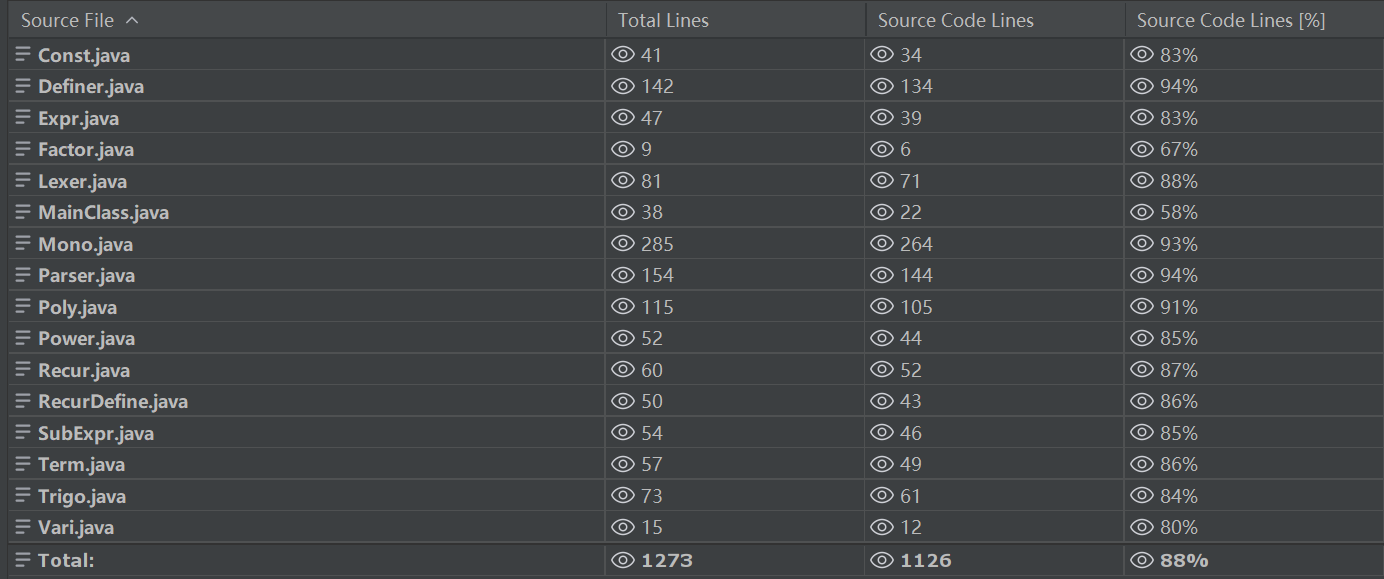
内聚度：设计要求高内聚低耦合，即 LCOM 值要小，FANIN 值要大，FANOUT 值要合理。

Type Name	LCOM	FANIN	FANOUT
Const	0	0	2
Expr	0	3	4
Factor	-1	8	1
RecurDefine	0	1	2
SubExpr	0.4	2	3
Term	0	2	3
Power	0	1	2
Recur	0.4	1	3
Trigo	0.222222	2	4
Vari	-1	0	1
MainClass	-1	0	4
Definer	0.4	1	4
Lexer	0	4	0
Parser	0	3	5
Mono	0.117647	7	4
Poly	0	9	2

递推函数解析部分内聚度不高，其余部分较好。

2.5 bug 分析

递推函数调用部分，参数为递推函数调用。出现这个 bug 在于简单的字符匹配出错，需要更多逻辑进行约束。

TLE 错误：字符串替换效率不高，需要对其进行化简再替换；三角函数容器以及单项式容器换用 HashMap。

此外，还可能出现读入递推函数定义时忘记处理空白项的情况。

3 第三次作业

3.1 需求说明

在之前的基础上，读入一系列自定义函数的定义以及一个包含幂函数、三角函数、自定义函数调用、求导算子的表达式，输出展开括号后的结果。

形式化表述新增：

自定义普通函数：属于变量因子，和自定义递推函数统称函数调用。例如：

1 2	g(x) = h(x) + 6 h(x) = g(x) * sin(x)

求导因子：属于因子。形式为 dx(x^2+sin(x)) ，括号内为任意表达式，展开为对表达式求导的结果。

3.2 项目结构

3.2.1 文件树

src
│  MainClass.java
│
├─expr
│  │  Const.java
│  │  Expr.java
│  │  Factor.java
│  │  SubExpr.java
│  │  Term.java
│  │
│  └─vari
│      │  Power.java
│      │  Trigo.java
│      │  Vari.java
│      │
│      └─call
│              Func.java
│              Ord.java
│              Recur.java
│
├─func
│      Define.java
│      OrdDefine.java
│      RecDefine.java
│
├─parser
│      Definer.java
│      Lexer.java
│      Parser.java
│
└─poly
        Mono.java
        Poly.java

3.2.2 UML 类图

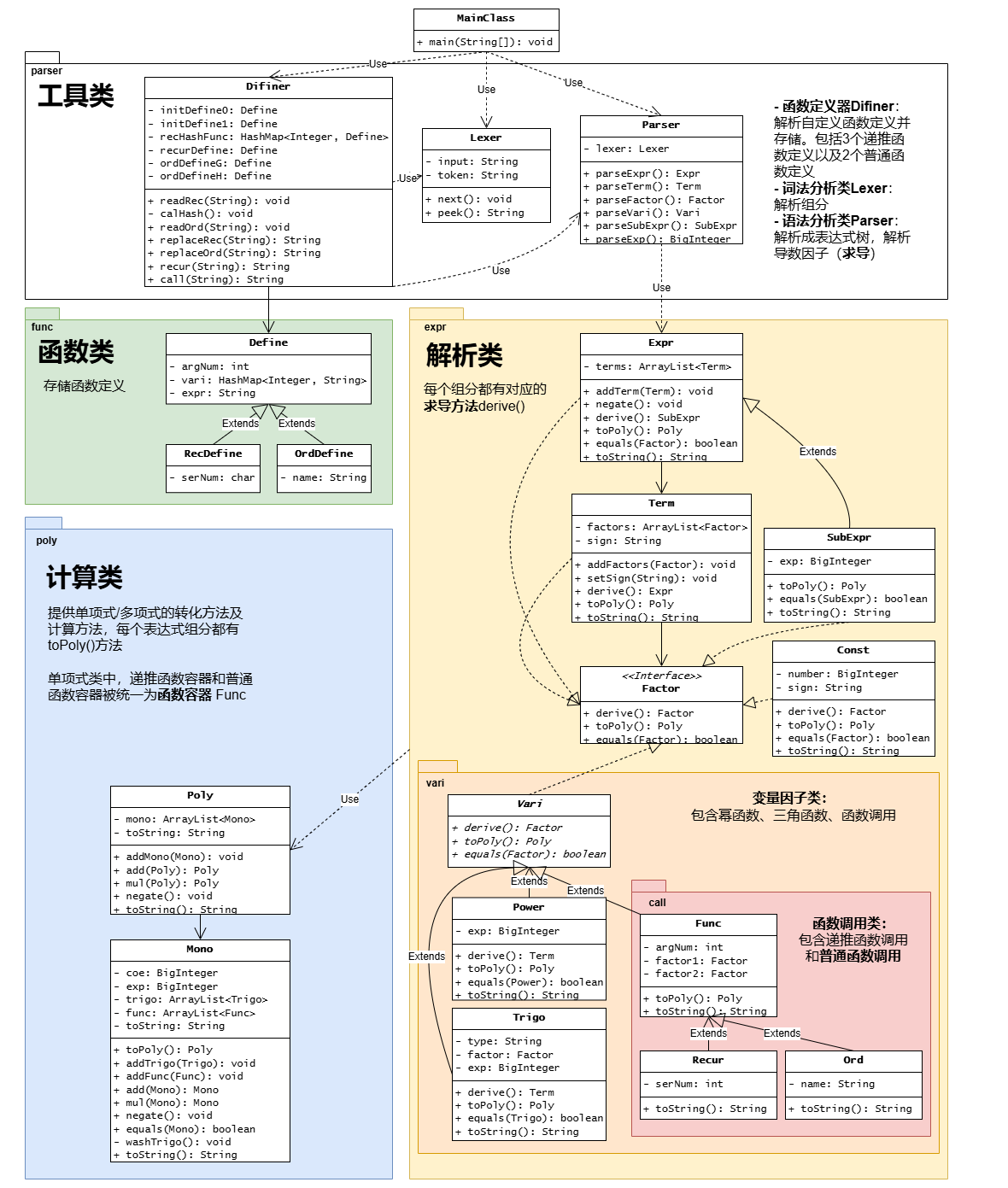
3.3 架构设计

第三次作业的架构与第二次作业如出一辙，没有很大的变动。

3.3.1 自定义普通函数

笔者还是沿用了第二次作业中处理自定义递推函数的方法，即字符串替换与表达式解析。

在面向对象设计方面，将自定义递推函数与自定义普通函数一起继承于同一个函数类，不同点在于递推函数需要记录递推序号，普通函数需要记录函数名称。

3.3.2 求导因子

求导操作在 Parser 中完成，每当 Lexer 读入一个 dx ，便调用之后的表达式的求导方法。因为求导因子属于因子，自然将其安排到 parseFactor 中。

// Parser.parseFactor()
// ...
else if (lexer.peek().equals("dx")) {  
    lexer.next(); // "("  
    lexer.next(); // Expr  
    Expr expr = parseExpr(); // ")"  
    String str = expr.toString();  
    Lexer lexer1 = new Lexer(str);  
    Parser parser = new Parser(lexer1);  
    expr = parser.parseExpr();  
    lexer.next(); // endOfDerive  
    return expr.derive();
}

接下来我们自顶向下地来看求导方法怎么实现。
首先在表达式类 Expr 中，求导方法是遍历每个项，调用他们的求导方法，并将它们加起来，返回一个表达式因子。这遵循的是求导的加法法则。

// Expr.java
public SubExpr derive() {  
    SubExpr expr = new SubExpr();  
    for (Term term : this.terms) {  
        Term term1 = new Term();  
        term1.addFactors(term.derive());  
        expr.addTerm(term1);  
    }  
    return expr;  
}

在项类 Term 中，求导方法是遍历每个因子，调用因子的求导方法，将其与其他因子的原函数相乘，最终这些东西相加。这遵循的是求导的乘法法则。

// Term.java
public Expr derive() {  
    Expr expr = new Expr();  
    for (int i = 0; i < factors.size(); i++) {  
        Term term = new Term();  
        term.addFactors(factors.get(i).derive());  
        for (int j = 0; j < factors.size(); j++) {  
            if (i != j) {  
                term.addFactors(factors.get(j));  
            }  
        }  
        expr.addTerm(term);  
    }  
    if (this.sign.equals("-")) {  
        expr.negate();  
    }  
    return expr;  
}

在因子 Factor 中，求导方法各有不同。常数因子求导直接返回一个常数 0；变量因子幂函数求导返回一个对应的 exp*x^(exp-1) 的项；变量因子三角函数求导，先改变本身的三角函数名称，再乘一个内部因子的求导结果，这遵循的是求导的链式法则。

// Trigo.java
public Term derive() {  
    Term term = new Term();  
    if (this.exp.equals(BigInteger.ZERO)) {  
        // ...
    } else {  
        BigInteger exp = this.exp;  
        // ...
        if (this.type.equals("sin")) {  
            term.addFactors(new Trigo("cos", this.factor, BigInteger.ONE));  
        } else {  
            term.addFactors(new Trigo("sin", this.factor, BigInteger.ONE));  
            term.setSign("-");  
        }  
        term.addFactors(this.factor.derive());  
    }  
    return term;  
}

至此，迭代新功能已经完成，接下来处理好各个部分之间可能存在的冲突便可。

3.4 性能度量

代码规模：

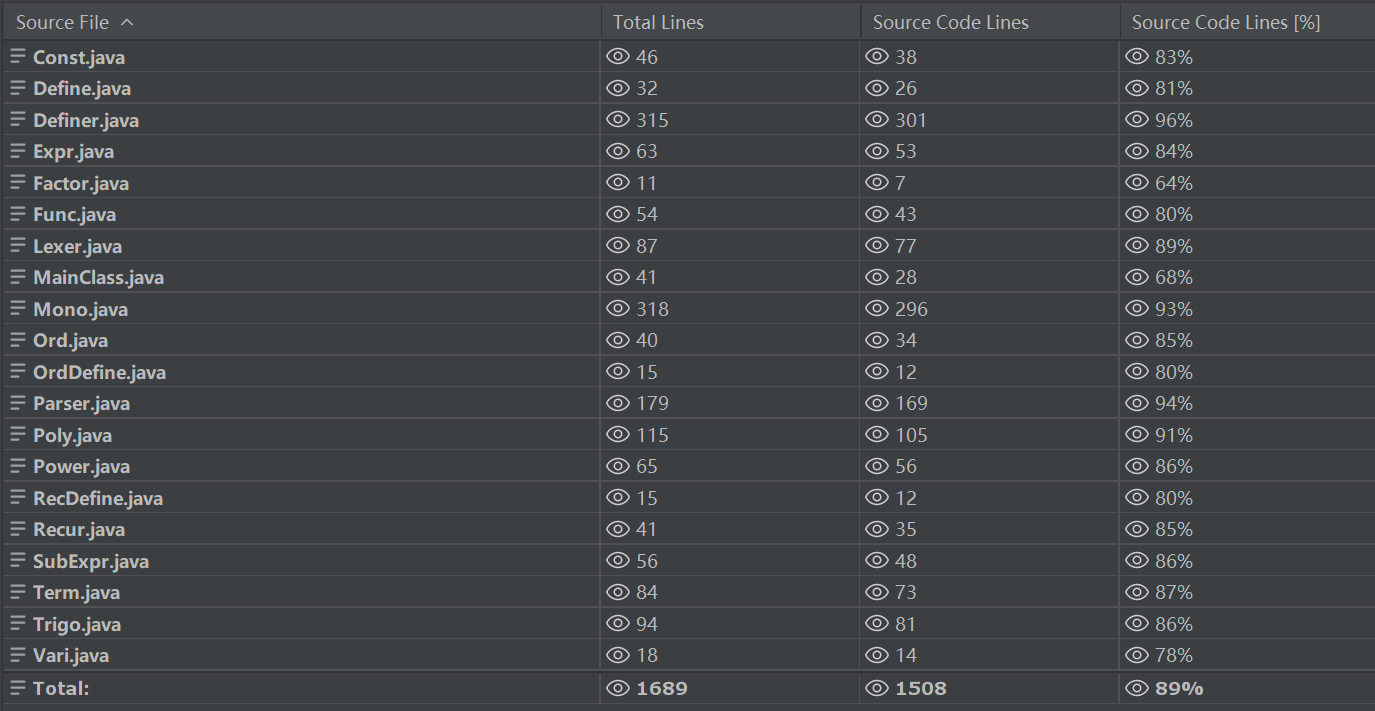
内聚度：设计要求高内聚低耦合，即 LCOM 值要小，FANIN 值要大，FANOUT 值要合理。

Type Name	LCOM	FANIN	FANOUT
Const	0.4	0	2
Expr	0	4	5
Factor	-1	10	1
SubExpr	0	3	3
Term	0.375	5	5
Func	0.375	1	3
Ord	0	0	1
Recur	0	0	1
Power	0	1	3
Trigo	0.2	2	5
Vari	-1	0	1
Define	0	1	0
OrdDefine	0	0	0
RecDefine	0	0	0
MainClass	-1	0	4
Definer	0	1	4
Lexer	0	3	0
Parser	0	3	6
Mono	0.111111	7	4
Poly	0	9	2

通过对比数据可以看出，三次作业的内聚度表现越来越好。

3.5 bug 分析

复杂度分析：LOC 表示代码行数，CC 表示圈复杂度。经过数据分析，以下方法的复杂度很高：

Type Name	MethodName	LOC	CC
Definer	readRec	42	8
Definer	recur2args	53	10
Mono	mul	50	11
Mono	powerToString	58	13
Mono	toString	71	13
Poly	add	50	13

这些函数有的是为了实现特殊的化简需求写了很多分支，有些是确实架构考虑上不充分导致的代码臃肿。这些函数大部分也确实是 bug 专业户（😓）

第三次作业相对于第二次作业对底层架构的改动很少，因此 bug 不太容易出现在之前已经完成的建模上，而是容易出现在不同单位之间的冲突，例如：

自定义递推函数定义内出现自定义普通函数的冲突；
自定义地推函数调用中出现自定义普通函数的传统；
求导因子中出现函数调用的冲突；
化简逻辑漏洞、不兼容新组分等（bushi）

新组分的添加导致旧组分产生新的 bug，笔者形象地将其比喻成 “排异反应”。产生这种 bug 的根本原因是编程者对代码的细节把握不够，抑或是考虑多种情况排列组合的能力不佳。

为了尽量减少这类 bug，评测机显得尤为重要，并且评测机的有效性也很关键（例如笔者室友的评测机因为没有经过人为特殊设置，导致随机出求导因子的概率很小，对其检测不充分，而求导因子中出现自定义函数的情况出现的概率更是微乎其微）。结合笔者上学期担任 C 语言程序设计助教的经验，数据生成采用完全随机是不太合理的，需要更多的人为考虑，主动地加入边界测试、压力测试，才能覆盖全面。好的测试方法也是 bug 的一大杀器。

4 心得体会

本单元让我狠狠的见识到了 OO 的强度（笑）。

关于重构。一定要舍得重构啊！在第一次作业后还好，咬咬牙也就重构了，但在第二、第三次作业的时候代码规模已经很大，忍着史山的膈应也不舍得全部推翻重来……就本人而言，最应该重构的部分是自定义函数的处理，其实也并不是全部推翻。希望今后的单元中我能以此说服自己更勤劳一些（😀）

关于评测机。评测机感觉不算一个加分项了，而是一个必须项了……现在的情况是中测乐呵呵，强测吃屎（x）。

第二单元的电梯调度部分更具挑战性，我会努力活下去的！

BaconToast's Shop

面向对象设计与构造OO：Unit1-表达式展开

0 前言

1 第一次作业

1.1 需求说明

1.2 项目结构

1.2.1 文件树

1.2.2 UML 类图

1.3 架构设计

1.3.1 预处理

1.3.2 得到后缀表达式

1.3.3 计算

1.3.4 化简

1.3.5 架构的优缺点

1.4 性能度量

1.5 bug 分析

2 第二次作业

2.1 需求说明

2.2 项目结构

2.2.1 文件树

2.2.2 UML 类图

2.3 架构设计

2.3.1 读取递推函数定义

2.3.2 替换递推函数调用

2.3.3 解析表达式

2.3.4 计算多项式并输出

2.3.5 架构的优缺点

2.4 性能度量

2.5 bug 分析

3 第三次作业

3.1 需求说明

3.2 项目结构

3.2.1 文件树

3.2.2 UML 类图

3.3 架构设计

3.3.1 自定义普通函数

3.3.2 求导因子

3.4 性能度量

3.5 bug 分析

4 心得体会

致谢